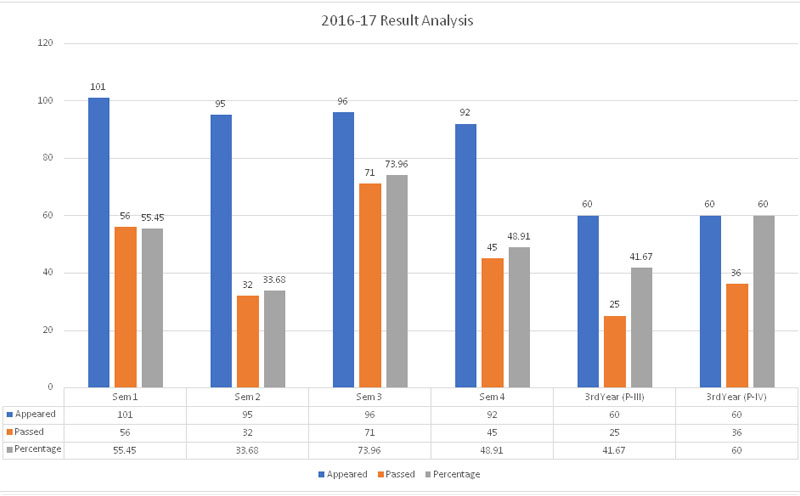
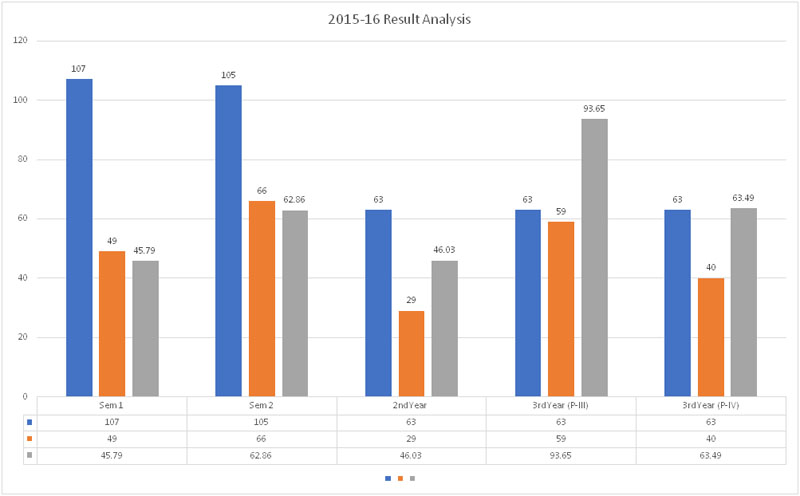
The department of Mathematics was established in 1972. Presently there are two sanctioned posts in the department. The faculty of the department enrich the students knowledge and improve Numerical skills to the needs of the society. The department extends its services to prepare the students in competitive examinations.
VISION: Imparting quality Mathematical Education and inculcating of the spirit of research through innovative teaching.
MISSION : To develop analytical skills and logical acumen for problem solving.
S.No |
Name |
Designation |
Qualification |
Photo |
Curricullum Vitae |
| 01 | Sri.M. Pamula Rao | Associate Professor | M.Sc., N.E.T. |  |
View CV |
| 02 | Dr. A. Gangadhara Rao | Associate Professor | M. Sc., M. Phil., Ph.D. |  |
View CV |
S.No |
Year of Starting |
Title of the Program |
LEVEL (UG, PG) |
Duration (Years) |
Sanctioned Annual Intake |
1 |
1995 |
B.Sc (Mathematics, Physics, Chemistry) |
UG |
3 |
40 |
2 |
1995 |
B.Sc (Mathematics, Physics, Computer Science) |
UG |
3 |
40 |
3 |
2015 |
B.Sc (Mathematics, Chemistry, Computer Science) |
UG |
3 |
60 |
4 |
2020 |
B.Sc (Mathematics, Chemistry, Industrial Chemistry) |
UG |
3 |
60 |
Mathematics Differential Equations
1 Define the differential equations.
2 Define order and degree of the differential equation.
3 Define the differential equations of first order and first degree and solving methods like linear equations, exact equations, equations reducible to exact form, Bernoulli’s equations.
4 Define the differential equation of first order but not of first degree and solving methods like equations solvable for p, equations solvable for y, equations solvable for x, Clairaut’s equations.
5 Construct the orthogonal trajectories for the curves belonging to Cartesian coordinates and polar coordinates.
6 Define the linear differential equations with constant coefficients and their general solutions.
7 Define the second order linear differential equations with variable coefficients and their solutions.
8 Solve the differential equations by using the method of variation of parameters.
9 Solve the Cauchy- Euler differential equations.
10 Solve the Legendre’s differential equations.
Mathematics Solid Geometry
1 Define the plane and describe the various forms of equations of the plane.
2 Find the angle between two planes, angle bisecting planes, the perpendicular distance from a point to a plane, the perpendicular distance between two parallel planes and intersection of two planes.
3 Define the pair of planes.
4 Find the angle between the pair of planes, distance between the pair of parallel planes.
5 Define the straight line and various forms of equations of lines.
6 Find the angle between two lines, image of a point in a plane, image of a line in a plane, foot of the perpendicular and perpendicular distance from a point to a plane and to a line.
7 Compute the angle between a line and a plane.
8 Describe the coplanar lines, skew lines.
9 Find the shortest distance and line of shortest distance between two skew lines.
10 Define sphere, discuss plane section of a sphere, great circle, small circle.
11 Explain tangent plane, tangent line, and secant line, plane of contact, pole and polar plane.
12 Discuss the angle of intersection of two spheres, orthogonal spheres.
13 Discuss coaxial system of spheres, limiting spheres.
14 Define cone and its properties.
15 Discuss guiding curve of cone, enveloping cone , reciprocal cone, right circular cone
16 Find the vertex of a cone.
17 Find the angle between the line of intersection of a plane and a cone.
18 Define cylinder and its properties.
19 Discuss enveloping cylinder, right circular cylinder.
Mathematics Abstract Algebra
1 Define binary operation and group structures in abstract algebra.
2 Describe finite and infinite groups.
3 Describe residues and residue classes.
4 Describe subgroups and their properties.
5 Describe cosets of subgroup of a group and their properties.
6 Describe Lagrange’s theorem on finite groups.
7 Describe normal subgroups and their properties.
8 Describe homomorphism and kernel of a homomorphism.
9 Describe fundamental theorem of homomorphism on groups.
10 Define permutation groups and their properties.
11 Describe Cayley’s theorem.
12 Define cyclic groups and their properties.
Mathematics Real Analysis
1 Define aggregate, boundedness, well ordering principle, completeness axiom, neighborhood property, limit point and some other properties of real numbers.
2 Define sequence of real numbers and different types of sequences.
3 Explain subsequences, boundedness of a sequence, lower and upper limit of a sequence.
4 Discuss the behavior of the geometric sequence.
5 Discuss the limit of a sequence and convergent and divergent sequences and their properties.
6 Verify the given sequence is convergent and divergent by using the behavior of Monotonic sequence.
7 Prove monotonic convergence theorem, sandwich theorem, Cesaro’s theorem, Cauchy first theorem on limits and Cauchy second theorem on limits.
8 Explain subsequences and upper and lower limits of a sequence.
9 Define an infinite series, convergent, divergent and oscillating series.
10 Discuss the behavior of geometric series, auxiliary series, limit comparison test, p-test, Cauchy nth root test, D’Alembert’s Ratio test, Cauchy condensation test. Verify the given series is convergent or divergent by using different types of tests.
11 Define an Alternating series and give some examples.
12 Discuss the behavior of Leibnitz test.
13 Define the absolutely and conditionally convergent series and verify the given series is either absolutely or conditionally convergent series.
14 Define continuity of a function at a point, partition of a closed interval.
15 Discuss Bolzano theorem, Intermediate value theorem.
16 Discuss the properties of continuous functions.
17 Define uniform continuity and discuss the properties of uniform continuous functions.
18 Define the derivative of a function at a point and give some examples.
19 Discuss the behavior of sign of the derivative of functions.
20 Discuss Darboux’s theorem and mean value theorems.
21 Define Riemann sums, Riemann integration and properties of Riemann integration.
22 Discuss the Necessary and Sufficient condition for Riemann integration.
23 Discuss the properties of Riemann integration.
24 Discuss the Fundamental Theorem of Integral Calculus and its application.
25 Discuss the First mean Theorem of Integral calculus.
26 Discuss the integral as the limit of a sum.
Mathematics Ring Theory and Vector Calculus
1 Define a ring and its properties.
2 Discuss commutative and non-commutative rings.
3 Discuss zero divisors in a ring.
4 Define integral domain, division ring, field and their properties.
5 Define Boolean ring and its properties.
6 Define characteristic of a ring.
7 Define sub ring, subfield, ideals of a ring and their properties.
8 Discuss principal ideal in a ring.
9 Define quotient ring and its properties.
10 Define homomorphism of rings and its properties.
11 Define prime ideal, maximal ideal and discuss their applications.
12 Define gradient, divergence and curl of function at a point.
13 Discuss line, surface and volume integrals.
14 Evaluate the integrals by using Gauss’s divergence theorem, Green’s theorem and Stoke’s theorem.
Mathematics Linear Algebra
1 Define Vector Space, linear sum, linear span and linear independent and linear dependent of vectors in a vector space.
2 Define basis and dimension of a vector space and quotient space and their properties.
3 Discuss the linear transformations, rank, nullity and rank-nullity theorem.
4 Find the characteristic equation, characteristic roots and characteristic vectors of a matrix.
5 Prove Cayley-Hamilton theorem.
6 Define inner product and inner product spaces.
7 Prove Schwartz inequality, Triangle inequality, parallelogram law in inner product spaces.
8 Define Orthogonal and Orthonormal vectors in inner product spaces.
9 Prove Gram-Schmidt ortogonalisation process, Bessel’s inequality, Parsevel’s identity.
Mathematics Numerical Analysis
1 Define numbers and their accuracy.
2 Define significant digits, error in numerical computations.
3 Discuss various types of errors.
4 Solve the algebraic and transcendental equations by using Bisection method Regula – Falsi method, Newton- Raphson method and iteration method.
5 Define basic concepts of the operators ∆, ∇, E, 𝞭, µ.
6 Find the difference of polynomials.
7 Find the missing terms by using finite differences.
8 Solve problems by using Newton’s forward and backward interpolation formulae.
9 Discuss central difference interpolation formulae.
10 Solve problems by using Gauss’s forward and backward interpolation formulae, Stirling‘s, Bessel’s and Everett’s formulae.
11 Explain divided differences.
12 Solve problems by using Newton’s divided difference formula and Lagrange’s formula.
Mathematics Integral Transforms
1 Solve the linear differential equations with constant coefficients by using Laplace transforms.
2 Solve the linear differential equations with variable coefficients by using Laplace transforms.
3 Solve the simultaneous linear differential equations by using Laplace transforms.
4 Solve the partial differential equations by using Laplace transforms.
5 Solve the integral equations by using Laplace transforms.
6 Discuss Fourier transforms, Fourier sine and cosine transforms.
7 Discuss finite Fourier sine and cosine transforms.
Mathematics Advanced Numerical Analysis
1 Fit the curves like straight line, exponential function, power function, second degree parabola by using method of least squares.
2 Explain Numerical Integration, trapezoidal rule, Simpson’s 1/3 and 3/8 rules, Boole’s rule, Weddle’s rule.
3 Find the integrals by using trapezoidal rule, Simpson’s 1/3 and 3/8 rules, Boole’s rule, Weddle’s rule.
4 Discuss Numerical differentiation.
5 Find the derivates by using Newton’s forward and backward interpolation formulae, Stirling‘s formula, Newton’s divided difference formula.
6 Find the maximum and minimum values for the tabular values by using numerical differentiation.
7 Solve the simultaneous linear system of equations by using Cramer’s rule, Matrix inversion method, Gauss’s elimination method, Gauss –Jordan method, factorization method, Gauss – Jacobi’s method, Gauss-Seidel method.
8 Solve the ordinary differential equations by using Picard’s method , Taylor’s method , Euler’s method, Euler’s modified method, Runge-Kutte method.
PSO1: Students are able to think in a critical manner.
PSO2: Students are able to know when there is a need for information, to be able to identify, locate, evaluate and effectively use that information for the issue or problem at hand.
PSO3: Students are able to understand formulae and develop mathematical arguments in a logical manner.
PSO4: Students are able to acquire good knowledge and understanding in Advanced areas of mathematics chosen by the students from the given courses.
PSO5: Students are able to understand, formulate and use qualitative models arising in social science, business and other contexts.
| Seminars |  |
Quizzes |  |
|
| Assignments |  |
Remedial Classes |  |
| Seminars |  |
Quizzes |  |
|
| Assignments |  |
Remedial Classes |  |
| S.No | Date | Conducted By | Name of The Activity | Details of Resource Person | No of Participants | Report |
|---|---|---|---|---|---|---|
| 01 | 22-12-2021 | Mathematics | National Mathematics day | Capt Dr M J SUBHAKAR | 139 | Click Here |
| 02 | 03-01-2022 to 07-01-2022 |
Mathematics | Student Exchange Programme | SNBT Degree College for Women, Repalle |
18 | Click Here |
| Remedial Classes |  |
Seminars |  |
| Remedial Classes |  |
Seminars |  |
| Remedial Classes |  |
Seminars |  |
| Remedial Classes |  |
Seminars |  |
| S.NO | Title of paper | Name of the author/s | Department | Name of journal | Year of Publication | ISBN / ISSN number | DOI Link |
| 1 | Some Results on F- Prime and F Semiprime ideals in Semigroups | Dr A. Gangadhara Rao | Mathematics | Stochastic Modeling &Apllications | Dec, 2021 | ISSN : 0972-3641 | https://www.mukpublication.com/si-2022.php |
| 2 | Fuzzy Regualr Partial Ordered Ternary Semigroups | Dr A. Gangadhara Rao | Mathematics | International Journal of Multidisciplinary Educational Research | May, 2022 | ISSN : 2277-7881 | http://ijmer.in.doi./2022/11.05.123 |
| 3 | Fuzzy Simple, FuzzyIdentity and Fuzzy Zero of a PO –Ternary Gamma Semigroups | Dr A. Gangadhara Rao | Mathematics | International Journal of Research in Engineering, Science and Management | June, 2022 | ISSN : 2581-5792 | https://www.ijresm.com |